Теорема Руденко
Спонсор проекта:
Вначале мы вспомним то, что общеизвестно, чтобы любой неискушённый в математике человек смог разобраться.
Понятие числа и множества является одним из основных понятий в математике. Это простые, первичные понятия, которые не определяются через другие.
Скажем так: множество — это совокупность объектов любой природы, называемых элементами множества.
Множество обозначают большими буквами: А, В, …. N. Элементы множества обозначают малыми буквами: а, b, … n.
Запись x ∈ А означает, что элемент х принадлежит множеству А.
Если х не входит во множество А, то пишут x ∉ А.
Запись ∀ х ∈ А: a означает, что для всех (для любого) из множества имеет место некоторое утверждение обозначенное α.
Запись ∃ х0 ∈ А:α означает, что существует (найдётся) такой элемент х из множества А, для которого справедливо утверждение обозначенное α.
Множества бывают дискретные и непрерывные, конечные и бесконечные.
В нашей записи мы будем рассматривать в основном только дискретные (штучные) множества, которые состоят из элементов (штук).
Пример дискретного множества: количество арбузов в Африке, где элементом множества является арбуз. Пример непрерывного множества: количество точек в портняжном метре закройщика.
Строго определить можно так: непрерывные множества это такие множества, где между любыми двумя точками (элементами) всегда найдётся третья.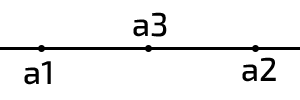 
Где а1 а2 отрезок, ∃а3 ∈ Δ а1 а2 при Δ а1 а2 → 0 в пределе, то есть непрерывное множество, заполняющее полностью весь отрезок а1 а2.
Иногда говорят: отрезок а1 а2 заполнен всюду плотно или, что существует взаимно-однозначное соответствие соответствие между числами R и точками отрезка а1 а2.
Что такое взаимно-однозначное соответствие? В нашем случае, это для любой точки числовой оси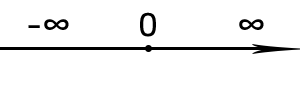 
найдётся число а принадлежащее а ∈ R, где R множество вещественных чисел R=(-∞ +∞) и, наоборот, для каждого числа а на числовой оси найдётся точка а.
Отсюда вывод: все непрерывные множества бесконечны.
Дискретные множества — это такие множества, что между двумя любыми элементами существует мера различия, например расстояние которое не может быть меньше какой-то величины Δ.
То есть между любыми элементами дискретного множества есть разрывы.
Дискретные (точечные) множества могут быть как конечные, так и бесконечные. Множество считается заданным, если о любом объекте можно сказать принадлежит он этому множеству или нет.
Объединение множеств
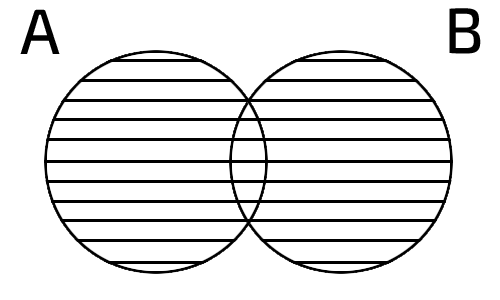
Множества можно комбинировать друг с другом и получать другие множества. Для этого используем операции: объединение множеств, пересечение множеств, дополнение к подмножеству, разность множеств, прямое произведение множеств.
Объединением множеств А и В называется множество, означаемое A∪B (или A+B) состоящее из элементов, которые принадлежат хотя бы одному из множеств А или В
A∪B={x ∈ A или x ∈ В}
Свойство объединения множеств
1. A∪B=B∪A
2. (A∪B)∪C=A∪(B∪C)
3. Если A∪B, то A∪B=В
4. A∪А=А
5. A∪Ø=А
Пересечение множеств
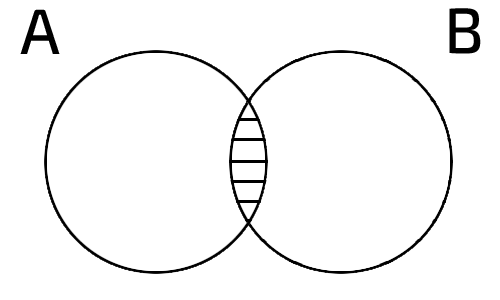
Свойство пересечения множеств
1. А⋂В=В⋂А
2. (А⋂В)⋂С=А⋂(В⋂С)
3. Если А⊂В, то А⋂В=А
4. А⋂А=А
5. А⋂Ø=Ø
Связь между операциями объединения и пересечения
1. А⋂(В∪С)=(А⋂В) ∪ (А⋂С)
2. А∪(В⋂С)=(А∪В) ⋂ (А∪С)
3. n(А∪В)=n(A)+n(B)-n(A⋂B)
Дополнение к множеству А во множестве V (если A⊂V) называется множество А всех тех элементов V, которые не принадлежат А.
A={x∈V и x∉A}.
Свойство дополнения к множеству
1. А⋂В∪А⋂В=А, то есть АВ+АВ=А
2. А∪А=V, то есть A+A=V
3. А⋂A=Ø 4. n(V)=n(A)+n(A)
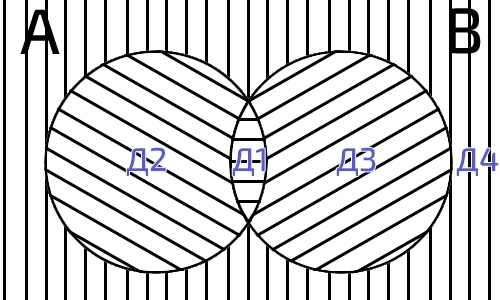
Любые два подмножества А и В множества V разбивают множество V на четыре области:
Д1=АВ Д2=АВ Д3=АВ Д4=АВ
Закон двойственности
1. Если А⊂V, В⊂V, то А⋂В=А∪В
2. Если А⊂V, В⊂V, то А∪В=АВ
Разность множеств
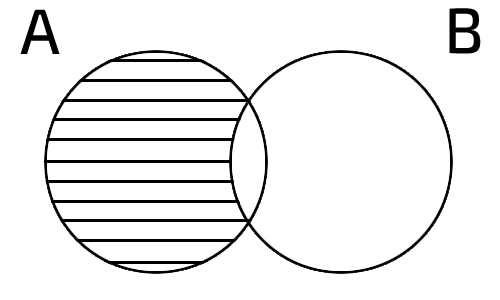
А\В={х∈A и х≠В}
Свойства разности множеств
1. А\В=А\(А⋂В)
2. Если А⊂V и V универсальное множество, то А=V\А
3. А\(В⋂С)=(А\В)∪(А\С)
4. А\(В∪С)=(А\В)⋂(А\С)
Прямое произведение множеств А и В называется множество, обозначаемое А·В и состоящее из всех упорядоченных пар вида (a,β), где а∈А, β∈В А·В={(a,β), a∈А и β∈В}.
Правила суммы и произведения
Пусть А и В два конечных не пересекающихся множества, содержащие n(А) и n(В) элементов соответственно.
• Правило суммы
Число n(А∪В) элементов множества А∪В вычисляется по формуле:
n(А∪В)=n(А)+n(В)-n(А⋂В).
Множество считается заданным, если о любом объекте можно сказать принадлежит он этому множеству или нет.
• Правило произведения
Число n(АВ) элементов множества АВ вычисляется по формуле:
n(АВ)=n(А)n(В).
Мощность множеств
Это вопрос касающейся количественной стороны множеств. Если множество конечное, то мы можем говорить о количестве его элементов, то есть, ответив на вопрос сколько, назвав конкретное натуральное число.
При этом легко определить в каком множестве элементов больше, а в каком меньше.
Сутью бесконечных множеств вопрос: «Сколько?» не имеет смысла — бесконечность не число!
Ещё более туманным является понятие > или < для бесконечных множеств. Понятие количества для бесконечных множеств заменяется понятием мощности. Мощность - инструмент количественного сравнения бесконечных множеств.
- Определение 1. Два множества называются эквивалентными, если между их элементами можно установить взаимно-однозначное соответствие.
Эквивалентные множества считаются равномощными, то есть имеющие одинаковую мощность.
- Определение 2. Множества, эквивалентные множеству натуральных чисел N, называются счётными.
Вывод. Счётные множества могут быть занумерованы, у каждого элемента есть свой номер.
Множество чётных чисел N2={2n} счётно. Соответствие N2⟷N описывает 2n⟷n.
Множество целых чисел счётно Z 0⟷1, 1⟷2, (-1)⟷3, 2⟷4, (-2)⟷5 …, то есть Z{0, 1, −1, 2, −2, 3….}.
Свойства счётных чисел
- Любое подмножество счётного множества либо конечно, либо счётно. Счётное множество наименьшее из бесконечных множеств.
- Объединение двух счётных множеств счётно.
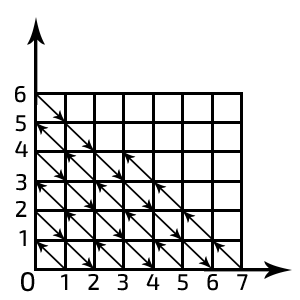
- И даже объединение счётного множества счётных множеств счётно.
Каждая точка плоскости получит свой натуральный номер и каждый натуральный номер получит свою точку, то есть существует взаимно-однозначное соответствие. Множество пар (P,S) из элементов двух счётных множеств P и S счётно.
Вывод. Множество Q = pq рациональных чисел счётно.
Теорема Руденко
N — множество натурального ряда. N={1, 2, 3, 4, 5, 6, 7, 8, 9, 10,….}, мощность |N| счётна.
Р — множество простых чисел (числа, которые делятся на 1 и на себя) Р={1, 2, 3, 5, 7, 11, 13, 17, 19,….}, так же считается счётными |Р|.
То есть, N множество натурального ряда было равномощно множеству простых чисел Р.
Докажем, что это не так. Действительно, любое натуральное число, которое не является простым, можно представить в виде разложения на простые числа.
То есть, простые числа являются как бы кирпичиками для разложения составных чисел и натуральный ряд представится в виде N1={1, 2, 3, 2·2, 5, 2·3, 7, 2·2·2, 3·3, 2·5,….}.
Значит N1~N это по сути одно и тоже, что и N1=N. Только в множестве N1 составные числа даны в виде разложения на простые множители.
Следовательно, любое подмножество простых чисел в общем виде запишем так m=an1·ak2·ap3·as4·….anv. ∈ N, где индекс внизу — номер простого числа, а степень — сколько раз простое число повторяется в разложении.
Пример для иллюстрации:
m=24·32·52·7·11 m=2·2·2·2·3·3·5·5·7·11·277200 ∈ N
Следовательно, любое и каждое подмножество простых чисел будет записано m ∈ N.
Обозначим через |Р| множество всех подмножеств простых чисел |Р| ⊂ N принадлежит натуральному ряду.
Ещё говорят |Р| булеан В(Р)⊂ N и наоборот любое натуральное число можно представить как одно из подмножеств простых чисел, то есть N ⊂ |Р|.
Пример: 19470⟷2·3·5·11·59.
Отсюда вывод: между множеством натурального ряда N и множеством всех подмножеств простых чисел, существует взаимно-однозначное соответствие, или говорят — они эквивалентны N~|Р|, то есть между элементами существует биекция.
N натуральный ряд ⟷ множество всех подмножеств простых чисел Р.
Проиллюстрируем: 1=1; 2=2; 3=3; 4=2·2; 5=5; 6=2·3; 7=7; 8=2·2·2; 9=3·3; 10=2·5; 11=11; 12=2·2·3; 13=13; 14=2·7; 15=3·5; 16=2·2·2·2; 17=17; 18=2·3·3; 19=19; 20=2·2·5; 21=3·7;…. и т. д.
Теперь согласно теореме Кантора, любое множество менее мощно, чем множество всех его подмножеств. Значит мощность натурального ряда счётна.
Следовательно, и мощность всех подмножеств простых чисел счётно.
Отсюда, согласно теореме Кантора следует, что множество простых чисел меньше по мощности натурального ряда, меньше счётного множества.
Вывод: существует хотя бы одно бесконечное множество по мощности меньше счётного.
Это множество простых чисел: Р={1; 2; 3; 5; 7; 11; 13; 17; 19;….}.
Следовательно, существует, по крайней мере, три вида бесконечных множеств различной мощности. Самое слабое из них множество простых чисел Р, мощность его обозначаем как |Р|.
Множество всех подмножеств простых чисел порождает более мощное множество — счётное множество, или как ещё говорят булеан В(Р) равномощен N. В(Р)~N.
Аналогично множество всех подмножеств натурального ряда N булеан В(N) порождает множество R=(-∞+∞) множество континуума В(N)~R.
И так повторим, что мы доказали.
То, что множество всех подмножеств простых чисел Р булеан В(Р) совпадает (порождает) натуральный ряд N, то есть В(Р)~N.
Между элементами В(Р) и элементами N существует биекция (взаимно-однозначное соответствие): В(Р)⟷N.
Но так как множество натурального ряда N счётно, то и булеан Р: В(Р) счётен.
Согласно теореме Кантора, если В(Р) множество всех подмножеств счётно, то мощность простых чисел Р меньше мощности N счётно.
Следовательно, множество простых чисел Р, во-первых бесконечно, и во-вторых по мощности меньше счётного |Р|<В(Р) или |Р|<|N|.
Покажем определённую закономерность: Простые числа Р Р={1, 2, 3, 5, 7, 11, 13, 17, 19, 23….}
Множество простых чисел мощность |Р|.
Натуральный ряд N N={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,….}
N натуральный ряд счётное множество мощность |N|.
Бесконечная прямая — мощность континуума.
Множество вещественных чисел R мощность континуума |R|. Р⊂N⊂R
Имеется зависимость: булеан В(Р)~N счётное множество, булеан В(N)~R континуум множеств.
Можно пофантазировать: булеан булеана В(В(Р))~R континуум или В2 (Р)~R продолжает континуум и ещё В3(Р)~ гиперконтинуум. Интуиция говорит, что других мощностей не бывает, но это пока гипотеза.
Приведём пару примеров в заключение:
- Простые числа разбросаны в натуральном ряду очень прихотливым образом, и не удивительно, что издревле математики стремились найти формулу простого числа. Самая простая формула простого числа выглядит, по-видимому, так: Р=Рn, где Рn — натуральный ряд, n∈ N, n=1, 2, 3, 4, 5,…., n — номер простого числа. Р=n-ное простое число.
То есть мы хотим для любого номера n∈ N найти n-ное простое число, назовём его К, К∈ Р. Получается, мы хотим найти биекцию между К∈ Р и n∈ N. Но К~n К⟷n. Биекции существовать не может, так как К принадлежит множеству простых чисел, а n принадлежит множеству N — счётному множеству.
Множества Р и N разномощны и не может между их элементами быть взаимно-обратного соответствия.
Поэтому формулы простых чисел не существует.
Многочисленные попытки многих математиков найти формулу простого числа потерпели крах, и другие пусть не пробуют — результат будет отрицательным. - Известна задача ещё более сложная, чем первая. Квадратура круга. Найти площадь квадрата равного площади круга. Такое соотношение есть, но построить его с помощью циркуля и линейки невозможно. Решается задача сотни лет, десятками учёных, а решения пока нет. Я покажу только одно: число π, отношение диаметра окружности к длине окружности, невозможно вычислить точно, до последней цифры.
Пусть диаметр Д=1, тогда длина окружности будет π=3,1415926…., то есть мы хотим сопоставить счётное множество Д=1 к трансцендентному π.
Д=1, π = 3,1415926….
Почему так относится длина окружности к диаметру одному Богу известно.
На этом всё.
P.S.: Послесловие
И так существует 3 различных по мощности бесконечных числовых множеств:
Простые числа : P = { 1;2;3;5;7;11;13;17;19;23…}
Мощностью: │Р│
Натуральные: Р ряд N
N { 1;2;3;4;5;6;7;8;9;10;11;12…}
Счетные множества мощности │N│
Бесконечные всюду плотный отрезок R € (0;1) или – R , +R
Мощность континуума │R│
Множество вещественных чисел : P Ϲ N Ϲ R имеется зависимость булеан B │ P │ ~ N
Счётное множество. Булеан B │N │ ~ R континуум
Зададимся вопросом существует ли еще бесконечные числовые множества другой мощности , и сейчас докажем , что других числовых множеств нет.
Схематически это изображается так :
Применим знаменитый принцип экономии , он действует в природе, обществе, науке БРИТВА ОККАМА.
Не надо множить сущее без необходимости или по другому отсечь всё лишнее.
Для нашего примера существует три бесконечных числовых множества:
Р – простые числа
N – натуральный ряд
R – множество континуума
И других решений нет.
В поперечном сечении схема имеет мощности числовых множеств имеет ядро ,что является областью простых чисел.
Кольцо охватывающее ядро , является областью натурального ряда и внешнее кольцо – это мощность континуума в продольном сечении схемы.
| R< | Область континуума |
| N< | Область натурального ряда 1;2;3;4;5;6;7;8;9;10;11;12;13;14;15;16 |
|
P |
Область простых чисел 1;2;3;5;7;11;13;17;19;23;29… |
Видим ,что по мощности
│P│< │N│< │R│ Булеан В|Р| ~ N
То есть область натурального ряда или что одно и тоже счётное множество N опирается на область простых чисел . И держит над собой область континуума,
Булеан B │N│ ~ R
Вот и вся тайна мощности бесконечных числовых множеств.